Задача двух тел. Уравнения движения в задаче двух тел

Уравнения движения в задаче двух тел

Движение двух материальных точек будем рассматривать в

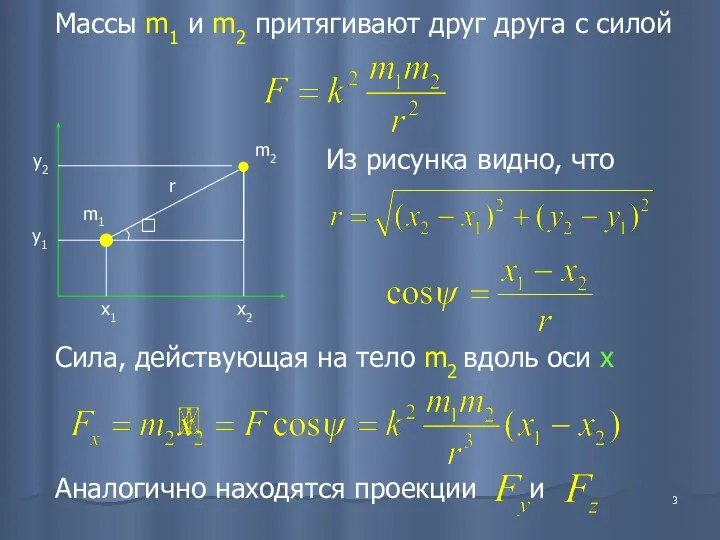
Массы m1 и m2 притягивают друг друга с силой

Сила, действующая на

Уравнения движения тела m2, притягиваемого телом m1 будут иметь вид

(1)

Аналогично находим уравнения движения тела m1 под влиянием притяжения от тела

Вычитая из (1) уравнения (2) находим уравнения движения тела m2 относительно

Вводя обозначения

и

окончательно получим

(3)

Интегралы площадей

Умножаем первое уравнение системы (3) на –y, второе – на

Интегралы площадей

В итоге получим:

Интегрируя эти соотношения, находим

(4)

Домножаем равенства (4) на z, x, y соответственно и складываем

(5)

получим:

Это уравнение плоскости, проходящей через начало координат. В этой плоскости происходит

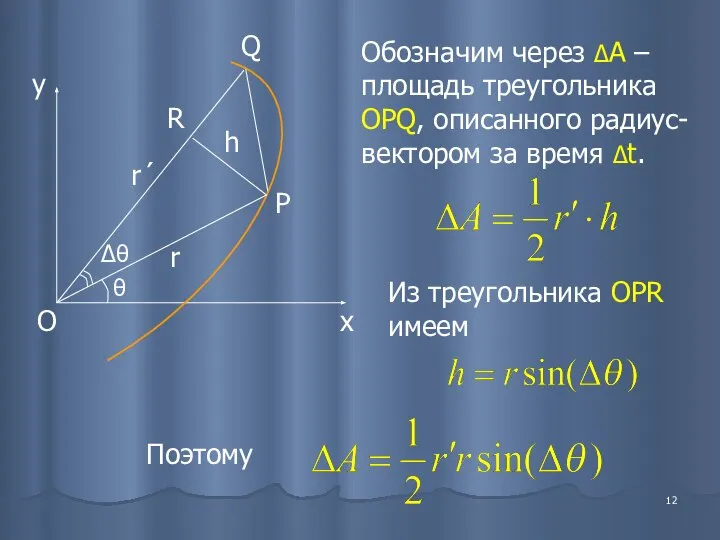
Обозначим через ΔА – площадь треугольника OPQ, описанного радиус-вектором за время

Перепишем последнее равенство в виде:

При

отношение площади треугольника

к площади сектора

,

В пределе при

имеем:

Это

Посмотрим теперь как будет выглядеть последнее выражение в прямоугольных координатах:

Отсюда:

В итоге

Постоянные а1, а2, а3 – проекции удвоенной секториальной скорости на плоскости

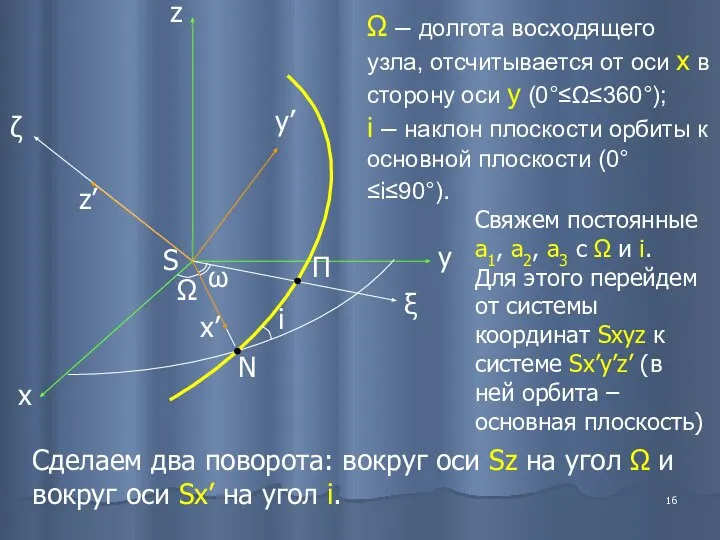
Ω – долгота восходящего узла, отсчитывается от оси x в сторону

Поворот вокруг оси Sz на угол Ω

(8)

В матричной форме этот поворот можно записать следующим образом:

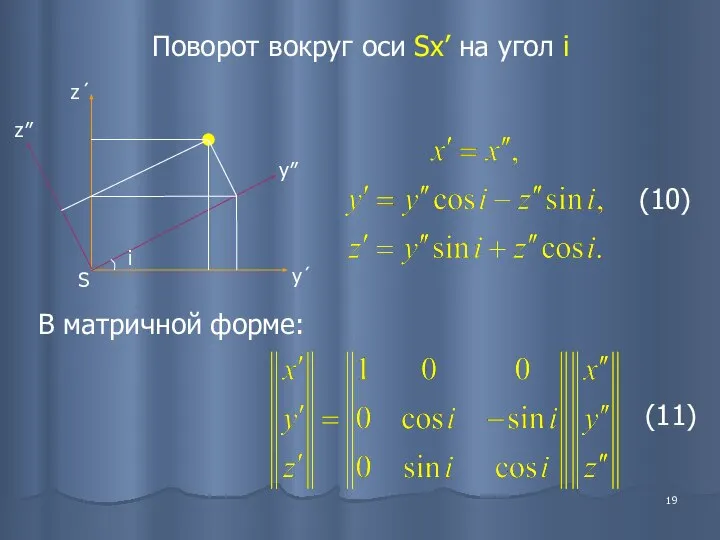
(9)

Поворот вокруг оси Sx’ на угол i

В матричной форме:

(10)

(11)

Таким образом, после двух поворотов, имеем:

Перемножив поворотные матрицы получим:

(12)

Так как компоненты удвоенной секториальной скорости в системе координат Oxyz есть

Перепишем теперь интегралы площадей:

(14)

Осталось связать здесь с элементами орбиты постоянную c.

Умножим первое, второе и третье уравнения системы (3) на

Сложив, получим:

можно переписать в виде:

Правую – в виде:

Левую часть равенства

Таким образом, имеем:

Интегрирование последнего выражения дает нам интеграл энергии:

(15)

Здесь

– постоянная интеграла

Так как движение происходит в плоскости, то координата z″=0, а радиус-вектор

Интеграл

Перейдем теперь от прямоугольных координат x″, y″ к полярным координатам r,

Из равенств (16) и (17) имеем

Таким образом

При помощи (16) можно найти

(18)

Уравнение (18) можно переписать в виде:

Преобразуем подкоренное выражение:

Обозначим:

Имеем:

Далее

Введем замену

Получим:

или

Последнее выражение можно проинтегрировать

где ω – постоянная интегрирования.

Отсюда

Но

Поэтому

или

Отсюда

Сравнивая теперь со стандартным уравнением конического сечения

где

– параметр орбиты

– большая полуось

–

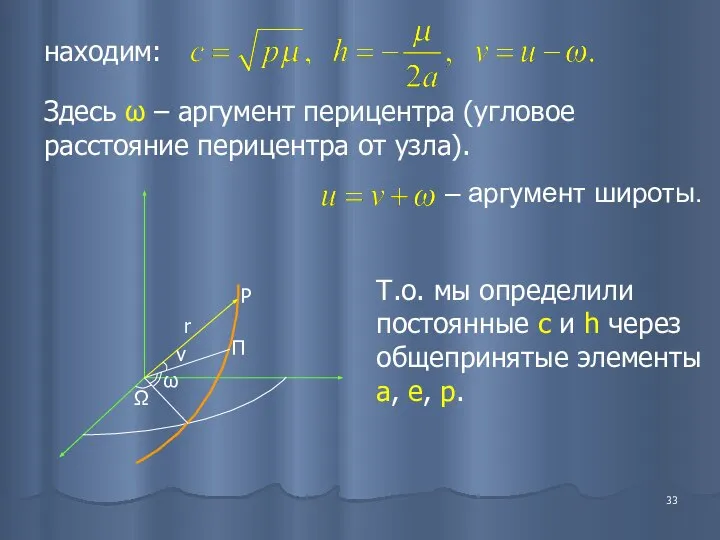
находим:

Здесь ω – аргумент перицентра (угловое расстояние перицентра от узла).

– аргумент

С этими постоянными интеграл энергии

Уравнение траектории

(19)

(20)

(21)

Уравнение интеграла площадей:

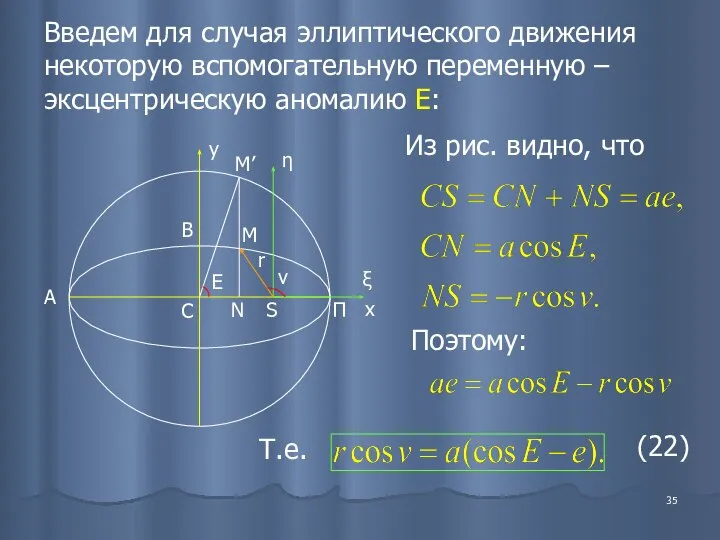
Введем для случая эллиптического движения некоторую вспомогательную переменную – эксцентрическую аномалию

Отношение малой и большой полуоси будет:

Здесь

Отсюда имеем:

(23)

Возводя (22) и (23) в

x2/a2+y2/b2=1 – уравнение эллипса
x'2/a2+y'2/a2=1 – уравнение окружности
x=x'
y=MN
y‘=M‘N

Подставляя (24) в (22) и (23), получим соотношения, связывающие истинную и

Делим первое на второе:

Используя тригонометрические соотношения

окончательно находим:

(26)

(25’)

Найдем теперь уравнение, связывающее переменную E со временем. Дифференцируя соотношение (26)

Из интеграла площадей (21)

Учитывая, что

Имеем

Используя также выражение для радиус-вектора (24)

Откуда имеем

и второе из соотношений (25’)

находим:

Интегрируя, находим:

(27)

Здесь

– постоянная интегрирования (момент прохождения через перигелий), а само уравнение

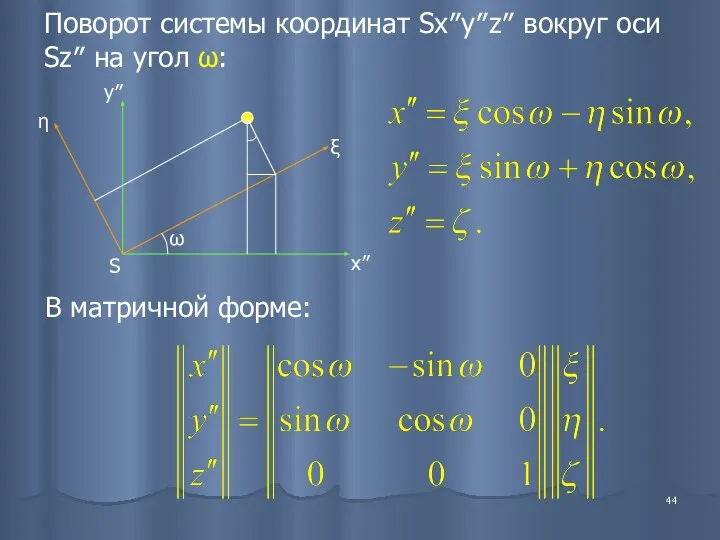
Поворот системы координат Sx″y″z″ вокруг оси Sz″ на угол ω:

В матричной

Таким образом, получить выражения для координат x, y, z через элементы

Так как движение в задаче двух тел происходит в плоскости, то

Уравнение Кеплера, связывающее эксцентрическую аномалию и время, обычно записывают в виде:

где

Величина

есть

Формулы, связывающие координаты x, y, z с элементами орбиты

Формулы для скоростей находим дифференцированием формул для координат

Формулы для координат и скоростей представляют также в виде

Проективные коэффициенты