Содержание
- 2. Из линейной алгебры известно: Равенства называются линейно независимыми, если никакое из них нельзя получить из других
- 3. Для реализации СМ необходимо 3 основных момента: Необходимо отыскать способ отыскания исходного допустимого решения. Должен быть
- 4. Рассмотрим задачу ЛП в стандартной форме при выполнении условий: max
- 5. Алгоритм решения задачи : Стандартная задача ЛП сводится к основной задаче. F= c1x1+…+cnxn→max a11x1+…+a1nxn+xn+1=b1 a11x1+…+a1nxn +xn+2=b2
- 6. Определяется начальное допустимое решение Для этого запишем систему ограничений в векторной форме x1A1+x2A2+…+ xnAn+xn+1An+1+…+ xn+mAn+m =A0
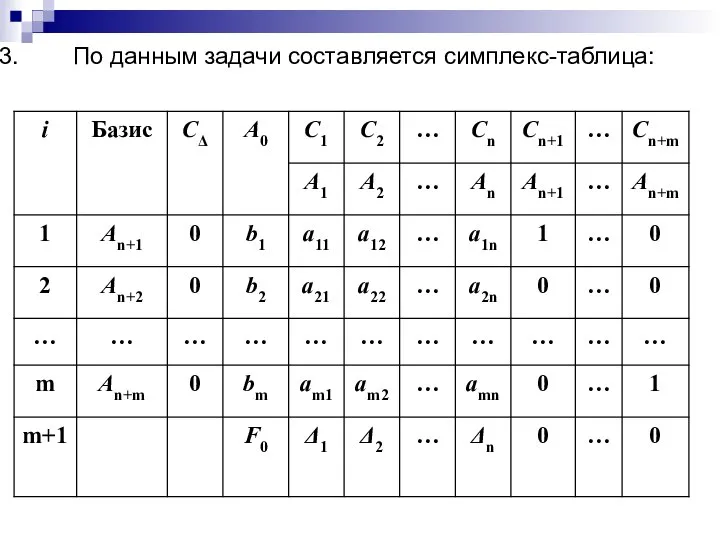
- 7. По данным задачи составляется симплекс-таблица:
- 8. В (m+1) –й строке в столбцах векторов Aj записываются значения ∆j = сiaij- значение целевой функции,
- 9. Полученное допустимое решение проверяется на оптимальность (в случае максимизации). Используются теоремы: Теорема2 Если для некоторого опорного
- 10. Наличие оптимальности проверяется по следующему признаку: Согласно теорем выясняется, имеется ли хотя бы одно отрицательное ∆j
- 11. В случае исследования целевой функции на минимум допустимое решение является оптимальным, если все разности ∆j ≤
- 12. Находится направляющий столбец и направляющая строка. Направляющий столбец определяется наибольшим по абсолютной величине отрицательным числом ∆j
- 13. Определяются положительные компоненты нового допустимого решения и коэффициенты разложения векторов Aj по векторам нового базиса и
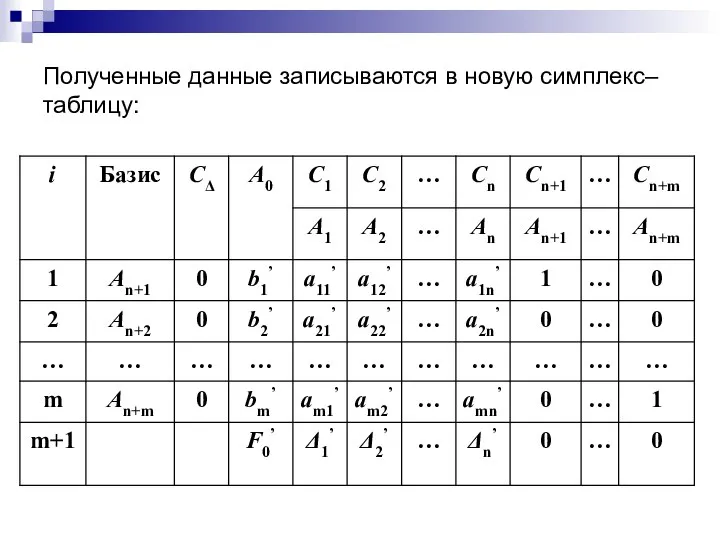
- 14. Полученные данные записываются в новую симплекс–таблицу:
- 15. Проверяют найденное допустимое решение на оптимальность Если решение не является оптимальным то возвращаются к п.5 ,
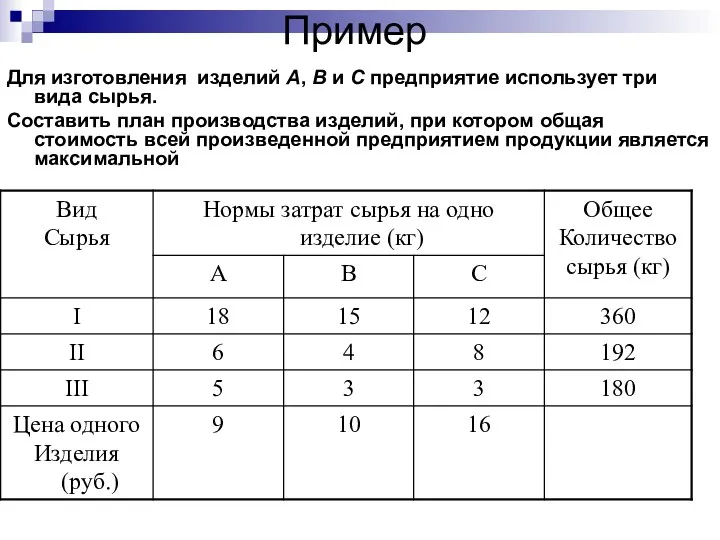
- 16. Пример Для изготовления изделий A, B и C предприятие использует три вида сырья. Составить план производства
- 17. Составим математическую модель задачи. max
- 18. Запишем эту задачу в форме основной задачи линейного программирования.
- 19. Полученную систему уравнений запишем в векторной форме:
- 20. Среди векторов имеются три единичных вектора , которые образуют базис трехмерного векторного пространства. Исходное решение задачи
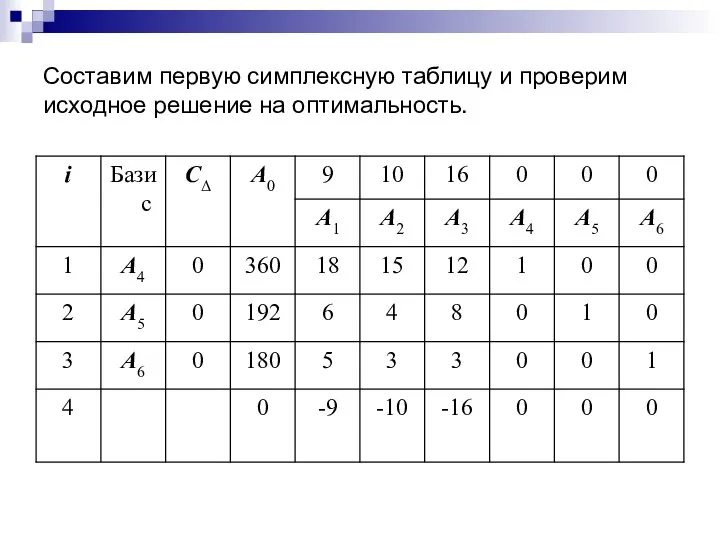
- 21. Составим первую симплексную таблицу и проверим исходное решение на оптимальность.
- 22. Значения, стоящие в четвертой строке симплексной таблицы вычисляются следующим образом:
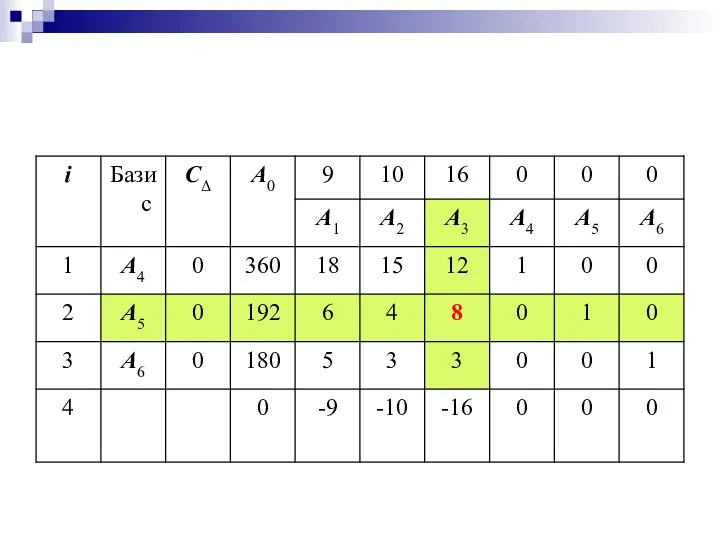
- 23. Исходное решение не является оптимальным, т.к. в 4-й строке таблицы имеются три отрицательных числа: -9, -10,
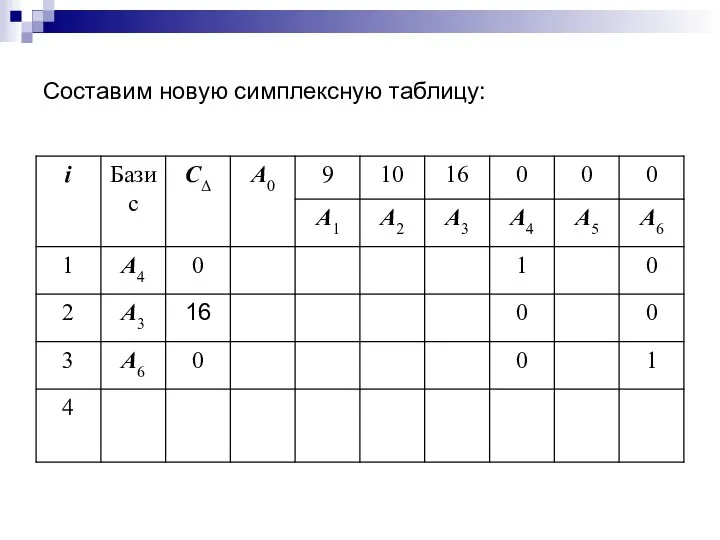
- 25. Составим новую симплексную таблицу:
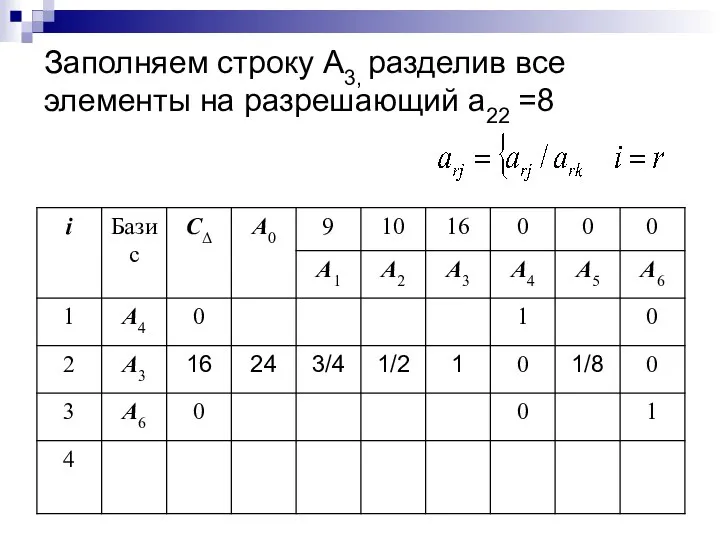
- 26. Заполняем строку A3, разделив все элементы на разрешающий а22 =8
- 27. Вычисление остальных элементов таблицы производим по рекуррентным формулам: В нашем случае k=3 r=2
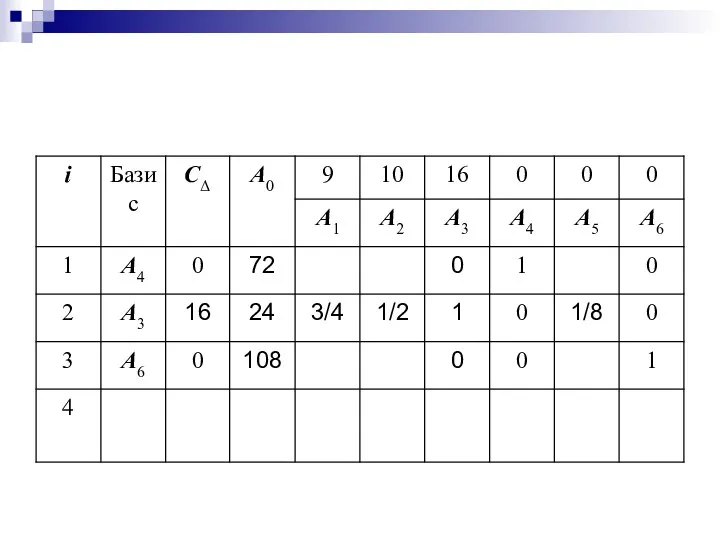
- 28. Тогда компоненты вектора A0 находятся
- 30. Вычислим компоненты вектора A1:
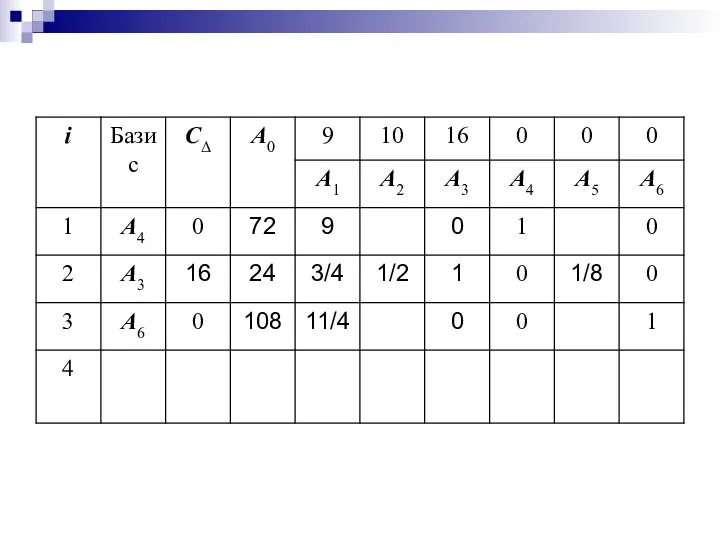
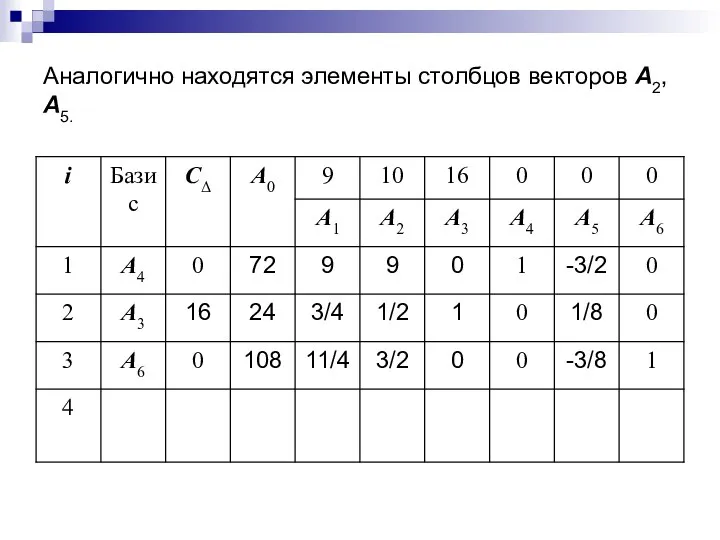
- 32. Аналогично находятся элементы столбцов векторов A2, A5.
- 33. Теперь заполним четвертую строку симплексной таблицы.
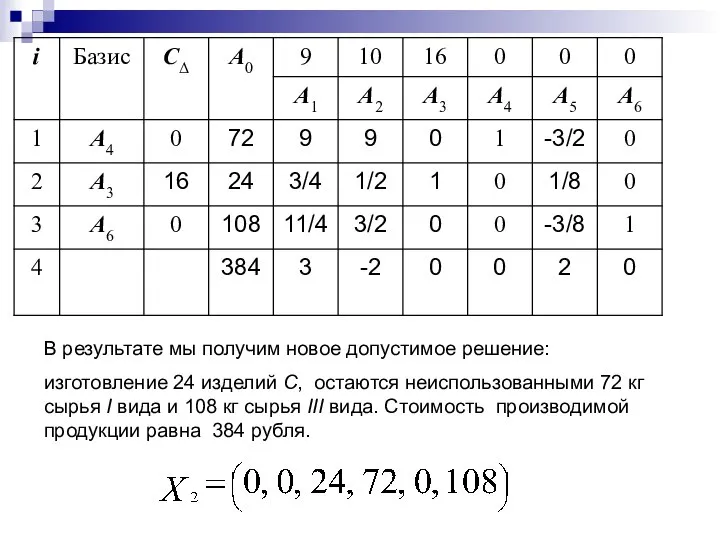
- 34. В результате мы получим новое допустимое решение: изготовление 24 изделий C, остаются неиспользованными 72 кг сырья
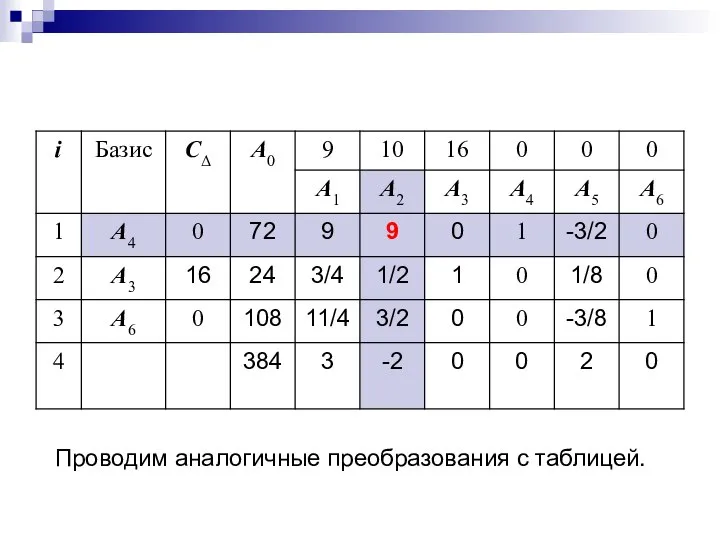
- 35. Решение X2 не является оптимальным, т.к. в 4-ой строке последней симплекс–таблице в столбце вектора A2 стоит
- 36. Проводим аналогичные преобразования с таблицей.
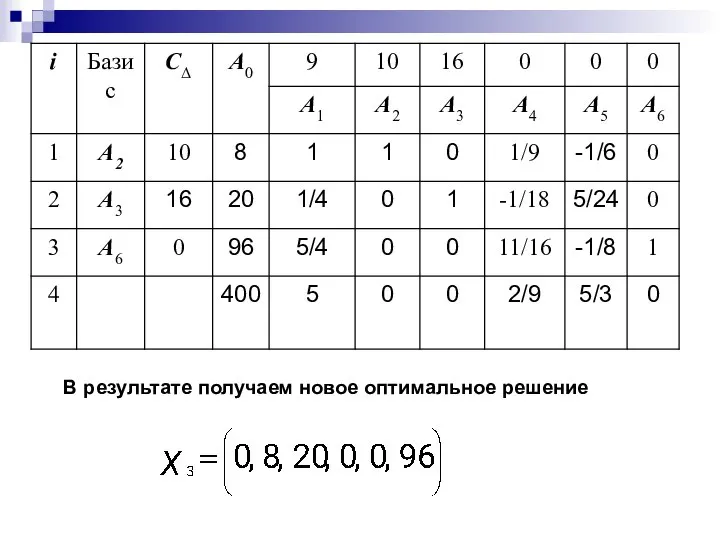
- 37. В результате получаем новое оптимальное решение
- 38. Ответ Это решение соответствует плану выпуска продукции, включающего изготовление 8 изделий B и 20 изделий C.
- 39. Вопросы В чем смысл симплекс-метода? Что необходимо для реализации СМ? Теорема о соответствии допустимых решений задачи
- 41. Скачать презентацию

























 Командная олимпиада “Высшая проба” 2019. Разбор задач
Командная олимпиада “Высшая проба” 2019. Разбор задач Сложение многочленов Если перед скобками стоит знак «плюс», то… Ответ: члены, стоящие в скобках своих знаков не меняют. Пример: 3х+(2а-5)=3х+2а-5.
Сложение многочленов Если перед скобками стоит знак «плюс», то… Ответ: члены, стоящие в скобках своих знаков не меняют. Пример: 3х+(2а-5)=3х+2а-5. Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна
Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Множественная регрессия
Множественная регрессия Сумма нескольких векторов
Сумма нескольких векторов Задача Дидоны Выполнил: Ронжина Мария Игоревна ученица 11 Г кл. МОУ «Лицей» г. Новотроицка. Руководитель: Поветкина Наталия Анатол
Задача Дидоны Выполнил: Ронжина Мария Игоревна ученица 11 Г кл. МОУ «Лицей» г. Новотроицка. Руководитель: Поветкина Наталия Анатол «Своя игра». Математическая викторина 5 класс
«Своя игра». Математическая викторина 5 класс Моделирование систем и процессов. Свойства, классификация математических моделей. Марковские случайные процессы. (Лекция 1)
Моделирование систем и процессов. Свойства, классификация математических моделей. Марковские случайные процессы. (Лекция 1) Математическая викторина 5-6 класс - Презентация по математике_
Математическая викторина 5-6 класс - Презентация по математике_ Деление с остатком
Деление с остатком Деление на двузначное число (4 класс)
Деление на двузначное число (4 класс) Systems of linear algebraic equations
Systems of linear algebraic equations Презентация на тему Методы решения экстремальных задач
Презентация на тему Методы решения экстремальных задач Презентация по математике "Теорема Пифагора" - скачать
Презентация по математике "Теорема Пифагора" - скачать  Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лекция 3)
Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лекция 3) Корень n-й степени из действительного числа (11 класс)
Корень n-й степени из действительного числа (11 класс) Урок 2. Новое из истории развития математики
Урок 2. Новое из истории развития математики Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра Координатная прямая
Координатная прямая Абсолютная величина вектора в пространстве
Абсолютная величина вектора в пространстве Арифметические действия с дробями
Арифметические действия с дробями Прибавление и вычитание числа 5
Прибавление и вычитание числа 5 Путешествие в сказочную страну. Урок - игра
Путешествие в сказочную страну. Урок - игра Сложение и вычитание десятичных дробей. (Урок 109)
Сложение и вычитание десятичных дробей. (Урок 109) Апроксимація експериментальних даних засобами табличного процесора
Апроксимація експериментальних даних засобами табличного процесора Решение задач с помощью пропорций. 7 класс
Решение задач с помощью пропорций. 7 класс Открытый урок в 1 классе по математике. Тема: Дециметр
Открытый урок в 1 классе по математике. Тема: Дециметр