Содержание
- 2. О возникновении т.н. «теории робастных систем» Основополагающей работой, определившей возникновение теории робастности, является теорема В.А. Харитонова.
- 3. Классификация простейших случаев неопределенности по видам характеристических полиномов для линейных стационарных систем Интервальная неопределенность – коэффициенты
- 4. Постановка задачи: где a(t) - произвольные функции времени, в том числе разрывные
- 5. Хорошо бы расследовать 1. Координатно-операторная обратная связь 1.1. Система с одним неопределенным параметром 1.2. Система с
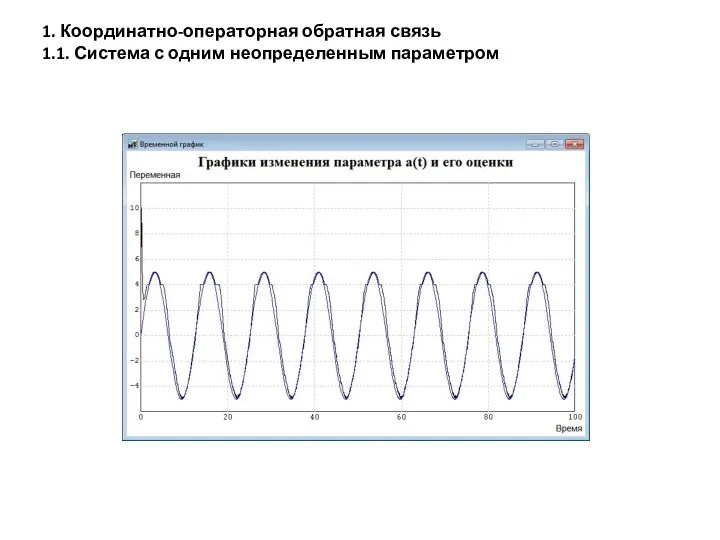
- 6. 1. Координатно-операторная обратная связь 1.1. Система с одним неопределенным параметром «Хрестоматийный» пример скаляризуем путем введения новой
- 7. t=time; init x1=1,x2=0,Miu_cp=0; ao=5; w=0.5; K=10; d=2; a=ao*sin(w*t); sigma=d*x1+x2; Ksi=sigma/x1; Miu=-K*sign(Ksi); Miu_cp'=5*(Miu-Miu_cp); a_oc=d^2-Miu_cp; u=-K*abs(x1)*sign(d*x1+x2); x1'=x2; x2'=a*x1+u;
- 8. 1. Координатно-операторная обратная связь 1.1. Система с одним неопределенным параметром
- 9. 1. Координатно-операторная обратная связь 1.1. Система с одним неопределенным параметром
- 10. Сделаем замену переменных 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами
- 11. где d характеризует качество стабилизации. Проведем следующие преобразования Тогда система уравнений примет вид 1. Координатно-операторная обратная
- 12. Если Е>0 то для стабилизации требуется Для того чтобы 1. Координатно-операторная обратная связь 1.2. Система с
- 13. Тригонометрический закон изменения параметров объекта. Рассматривается стабилизация модели вида 1. Координатно-операторная обратная связь 1.2. Система с
- 14. 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами Тригонометрический закон изменения параметров
- 15. 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами Тригонометрический закон изменения параметров
- 16. Тригонометрический закон изменения параметров объекта. 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными
- 17. , где 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами Дифференциальный закон
- 18. 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами Дифференциальный закон изменения параметров
- 19. 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами Дифференциальный закон изменения параметров
- 20. 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами Дифференциальный закон изменения параметров
- 21. 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами Дифференциальный закон изменения параметров
- 22. ,где 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами Дифференциальный с sign
- 23. 1. Координатно-операторная обратная связь 1.2. Система с двумя и более неопределенными параметрами Дифференциальный с sign закон
- 24. Дифференциальный с sign закон изменения параметров объекта 1. Координатно-операторная обратная связь 1.2. Система с двумя и
- 25. Дифференциальный с sign закон изменения параметров объекта 1. Координатно-операторная обратная связь 1.2. Система с двумя и
- 26. Дифференциальный с sign закон изменения параметров объекта 1. Координатно-операторная обратная связь 1.2. Система с двумя и
- 27. 1. Координатно-операторная обратная связь 1.3. Система, представленная в «Фробениусовой» форме с неограниченным числом неопределенных параметров Введем
- 28. 1. Координатно-операторная обратная связь 1.3. Система, представленная в Фробениусовой форме с неограниченным числом неопределенных параметров Стоит
- 29. 1. Координатно-операторная обратная связь 1.3. Система с 4- мя неопределенными параметрами Состояние объекта управление
- 30. в отличие от п. 3, вводим координатную ошибку следующим соотношением 2. Операторная обратная связь 2.1. Система
- 31. 2. Операторная обратная связь 2.1. Система с одним неопределенными параметрами График изменения состояний объекта График изменения
- 32. 2. Операторная обратная связь 2.2. Система с неограниченным числом неопределенными параметров Заметим что рассматриваемая матрица является
- 33. 2. Операторная обратная связь 2.2. Система с неограниченным числом неопределенными параметров Тогда уравнение замкнутой системы примет
- 34. 2. Операторная обратная связь 2.2. Система с неограниченным числом неопределенными параметров Теперь можно найти значения обеспечивающие
- 35. 2. Операторная обратная связь 2.2. Система с неограниченным числом неопределенными параметров Произведем синтез регулятора для системы
- 36. 2. Операторная обратная связь 2.2. Система с неограниченным числом неопределенными параметров Состояние объекта управление
- 40. Скачать презентацию




































 Сложение и вычитание многочленов. 7 класс
Сложение и вычитание многочленов. 7 класс Measures of variation. Week 4 (2)
Measures of variation. Week 4 (2) Регрессионный анализ. Эмпирические модели. Понятия регрессии. Уравнение линейной регрессии. (Лекция 9)
Регрессионный анализ. Эмпирические модели. Понятия регрессии. Уравнение линейной регрессии. (Лекция 9) Теорема Пифагора
Теорема Пифагора Математический бой. Конкурсы
Математический бой. Конкурсы Прямая пропорциональность и её график. 7 класс
Прямая пропорциональность и её график. 7 класс Вычислить интеграл от функции комплексного переменного по данной кривой
Вычислить интеграл от функции комплексного переменного по данной кривой Подготовка к контрольной работе по алгебре. (9 класс)
Подготовка к контрольной работе по алгебре. (9 класс) Задачи на части
Задачи на части Пирамида. 10 класс
Пирамида. 10 класс Функции у=|x| и ей график
Функции у=|x| и ей график Определенный интеграл. Приложения определенного интеграла
Определенный интеграл. Приложения определенного интеграла Проверка домашнего задания
Проверка домашнего задания Проценты. Сравнение с целым
Проценты. Сравнение с целым Счёт десятками
Счёт десятками Метод логических рассуждений
Метод логических рассуждений Решение логических задач
Решение логических задач Обслуговування викликів у СРІ типу M/M/v/L
Обслуговування викликів у СРІ типу M/M/v/L Разбор заданий В4 Работа выполнена ученицей 11 «А» класса МОУ «СОШ №47» г.Саратова Акимовой Светланой Константиновной Руководите
Разбор заданий В4 Работа выполнена ученицей 11 «А» класса МОУ «СОШ №47» г.Саратова Акимовой Светланой Константиновной Руководите Правильные многоугольники в нашей жизни
Правильные многоугольники в нашей жизни Задачи на построение
Задачи на построение Числовые и алгебраические выражения
Числовые и алгебраические выражения Компоненты математических действий
Компоненты математических действий Математические предложения
Математические предложения Олимпиадная математика. Доказательство от противного
Олимпиадная математика. Доказательство от противного Презентация по математике "Числа в различных системах счисления" - скачать бесплатно
Презентация по математике "Числа в различных системах счисления" - скачать бесплатно Удивительные десятичные дроби. 5 класс
Удивительные десятичные дроби. 5 класс Координатная плоскость
Координатная плоскость