Содержание
- 2. Вопросы: 4.1. Спецификация уравнения регрессии и ошибки спецификации. 4.2. Мультиколлинеарность: способы выявления и устранения 4.3. Фиктивные
- 3. Модель множественной линейной регрессии в матричном виде
- 9. Уравнение множественной линейной регрессии в матричном виде
- 10. Метод наименьших квадратов
- 11. Условия теоремы Гаусса-Маркова 1. i=1,…,n 2. при i=j 3. при i≠j 4. i=1,…,n
- 12. Гомоскедастичность Гетероскедастичность
- 13. Условия теоремы Гаусса-Маркова при i=j 2,3 при i≠j
- 14. Условия теоремы Гаусса-Маркова или где I – единичная матрица
- 15. Мультиколлинеарность Способы выявления и устранения
- 16. Признаки наличия мультиколлинеарности 1. Небольшое изменение исходных данных сильно изменяет значения оценок коэффициентов
- 17. Признаки наличия мультиколлинеарности 2. Стандартные ошибки коэффициентов очень велики (коэффициенты стат. незначимы), а модель в целом
- 18. Признаки наличия мультиколлинеарности 3. Значения коэффициентов неправильны с точки зрения экономической теории
- 19. Способы выявления мультиколлинеарности: 1. Вычисление матрицы парных коэффициентов корреляции для всех объясняющих переменных. 2. Расчет фактора
- 20. Матрица парных коэффициентов корреляции
- 21. Фактор инфляции вариации
- 23. Методы устранения мультиколлинеарности: 1. Удаление коллинеарных переменных. 2. Исправление выборки (проверка ее репрезентативности). 3. Преобразование переменных,
- 24. Случай 1. Исключены существенные переменные.
- 25. Случай 2. Включены несущественные переменные.
- 26. Информационные критерии Акаике и Шварца
- 27. Информационные критерии Хеннана-Куинна
- 28. Фиктивные переменные в регрессионных моделях dummy
- 29. X=0 если женский x=1 если мужской
- 30. X=0 если женский x=1 если мужской
- 31. X=0 если женский x=1 если мужской
- 34. неправильно
- 35. правильно
- 37. Фиктивные переменные позволяют строить и оценивать так называемые кусочно-линейные модели, которые можно применять для исследования структурных
- 38. Пусть в момент времени tо произошли некие структурные изменения и линия регрессии будет отличаться от той,
- 41. Регрессионная линия (рис) имеет коэффициент наклона β1 для t ≤ to и наклон β1+β2 для t
- 42. Тестируя стандартную гипотезу β2=0 мы проверяем предположение о том, что фактически структурные изменения не повлияли на
- 44. ГЕТЕРОСКЕДАСТИЧНОСТЬ ОСТАТКОВ
- 45. Гомоскедастичность при i=j
- 46. Гетероскедастичность при i=j
- 47. Последствия гетероскедастичности Основное последствие гетероскедастичности заключается в получении неэффективных оценок параметров модели регрессии, что проявляется в
- 48. Способы обнаружения гетероскедастичности Графики Тесты
- 49. Примеры гетероскедастичности
- 50. Примеры гетероскедастичности
- 51. Примеры гетероскедастичности
- 52. Тесты на гетероскедастичность 1. Бартлетта 2. Голдфелда-Квандта 3. Уайта 4. Бреуша-Пагана 5. Глейзера
- 53. Остатки:
- 54. Вне зависимости от используемых тестов необходимо сформулировать гипотезы: при i=j остатки гомоскедастичны при i=j остатки гетероскедастичны
- 55. Тест Голдфелда-Куандта. 1. Упорядочить наблюдения по убыванию той независимой переменной, относительно которой есть подозрение на гетероскедастичность.
- 56. Тест Голдфелда-Куандта. 2. Опустить v наблюдений, оказавшихся в центре (v должно быть примерно равно четверти общего
- 57. Тест Голдфелда-Куандта. 3. Оценить отдельно обыкновенным МНК регрессии на первых (n−v)/2 наблюдениях и на последних (n−v)/2
- 58. Тест Голдфелда-Куандта. 4. Найти SSE1 и SSE2 – суммы квадратов остатков (ошибок) для первой и второй
- 59. Тест Голдфелда-Куандта. 6. Найти Fкр. по таблице распределения Фишера по уровню значимости α и числу степеней
- 60. Если Fнабл.>Fкр., то нулевая гипотеза отклоняется в пользу альтернативной о гетероскедастичности остатков. Иначе оснований отклонять нулевую
- 61. Тест Уайта. 1. Оцениваем параметры исходной модели, получаем уравнение регрессии
- 62. Тест Уайта. 2. Находим остатки 3. Находим квадраты остатков
- 63. Тест Уайта. 4. Строим вспомогательную регрессию, в которой в качестве зависимой переменной выступают квадраты остатков ,
- 64. Тест Уайта. Например, для двухфакторной модели вспомогательная регрессия будет иметь вид:
- 65. Тест Уайта. 5. Оцениваем вспомогательную регрессию и находим R2 вспомогательной регрессии. 6. Вычисляем наблюдаемое значение
- 66. Тест Уайта. 7. По таблице распределения Пирсона по уровню значимости α и числу степеней свободы k
- 67. Тест Уайта. 8. Сравниваем наблюдаемое и критическое значения.
- 68. Тест Уайта. Если , нельзя отклонить нулевую гипотезу об отсутствии гетероскедастичности. Если , нулевая гипотеза отклоняется
- 69. Тест Уайта (упрощенный) Отличается от классического вспомогательной регрессией, в которой в качестве зависимой переменной выступают квадраты
- 70. Тест Уайта (упрощенный). Тогда вспомогательная регрессия будет иметь вид:
- 71. Тест Уайта (упрощенный). А число степеней свободы k = 2-1=1
- 72. Критерий Бартлетта.
- 73. Критерий Бартлетта.
- 75. Обобщенный МНК Отличается от обычного МНК в изменении предположений о поведении случайной ошибки. Обычный МНК: Обобщенный
- 76. Обобщенный МНК Или Обычный МНК: при i=j при i≠j Обобщенный МНК: при i=j при i≠j
- 77. Обобщенный МНК Если есть только гетероскедастичность, то: Обобщенный МНК: при i=j
- 78. Обобщенный МНК Критерий минимизации суммы квадратов ошибок МНК заменяется на другой – минимизация обобщенной суммы квадратов
- 79. Обобщенный МНК Соответственно усложняется вид системы уравнений для определения оценок коэффициентов. ОМНК позволяет получить линейные несмещенные
- 80. Обобщенный МНК Соответственно усложняется вид системы уравнений для определения оценок коэффициентов. ОМНК позволяет получить линейные несмещенные
- 81. Обобщенный МНК
- 82. Обобщенный МНК Оценки МНК получаются по формуле Оценки ОМНК получаются по формуле
- 83. Обобщенный МНК Для применения ОМНК необходимо знать элементы матрицы Ω, что на практике случается крайне редко.
- 84. Взвешенный МНК Предположим, что нам известны значения величин Тогда исходную модель разделим на σi:
- 85. Исходная модель
- 86. где причем при
- 87. Взвешенный МНК Для получения оценок неизвестных дисперсий будем предполагать, что они пропорциональны некоторым числам где σ2
- 88. Взвешенный МНК Принимая различные гипотезы относительно характера гетероскедастичности, будем иметь соответствующие значения λi. Если дисперсия случайного
- 89. Взвешенный МНК Если дисперсия случайного члена пропорциональна X, так что то
- 90. Взвешенный МНК Если предположить, что дисперсия случайного члена пропорциональна то необходимо преобразовать модель следующим образом:
- 91. Существуют также и другие методы коррекции модели на гетероскедастичность, в частности, состоятельное оценивание стандартных ошибок. Известны
- 92. Стандартные ошибки в форме Ньюи-Веста. Пусть в матрице ковариаций Ω ненулевые элементы стоят не только на
- 93. Автокорреляция в остатках
- 94. пространственные данные – cross-sectional data; временные ряды данных – time-series data
- 95. Условие отсутствия автокорреляции при i≠j или где I – единичная матрица
- 96. Причины автокорреляции Стохастические зависимости между значениями случайных ошибок – автокорреляция ошибок. Ее причинами являются: влияние некоторых
- 97. Последствия автокорреляции: 1. Выборочные дисперсии полученных оценок коэффициентов будут больше по сравнению с дисперсиями по альтернативным
- 98. Стандартные ошибки коэффициентов будут оценены неправильно, т.е. оценки коэффициентов будут неэффективны. Выводы о значимости оценок коэффициентов
- 99. Можно рассматривать так называемую корреляцию сериями (автокорреляцию), когда зависимость между ошибками, отстоящими на некоторое количество шагов
- 100. система координат (ei; ei-s)
- 103. et t Пример графика остатков по наблюдениям при положительной автокорреляции
- 104. Пример графика остатков по наблюдениям при отрицательной автокорреляции et t
- 106. Тестирование на наличие автокорреляции. Для проверки гипотезы о существовании линейной автокорреляции первого порядка, которая чаще всего
- 107. Критерий Дарбина-Уотсона.
- 108. Тестирование на наличие автокорреляции. Критерий Дарбина-Уотсона предназначен для моделей с детерминированными регрессорами X и не применим
- 110. Коэффициент автокорреляции первого порядка
- 112. По таблице Дарбина-Уотсона определяются две критические точки: верхняя dU и нижняя dL.
- 113. Границы интервала (dl и du) критических значений критерия Дарбина-Уотсона при уровне значимости α=0,05 (n - объем
- 114. 2 4 0 dL dU dcrit положительная автокорреляция отрицательная автокорреляция нет автокорреляции dcrit Области статистических решений
- 116. Методы устранения автокорреляции Кохрейна-Оркатта Хилдрета-Лу Дарбина
- 117. Запишем регрессию (1):
- 118. В момент времени t-1 имеем (2):
- 119. Умножим уравнение (2) на коэффициент автокорреляции ρ:
- 120. Вычтем уравнение (2) из уравнения (1)
- 124. Предположим, что остатки ui удовлетворяют следующему уравнению: ui=ρui-1+ςi, i=2,...,n, (4.11) представляющему собой авторегрессионную модель первого порядка,
- 125. Оценивание регрессии при наличии автокорреляции. Метод 1. Отказавшись от определения величины ρ статистически, можно положить ρ=0,5;
- 126. Метод 3. Итеративная процедура Кохрейна-Оркатта. а) Оценивается регрессия с исходными не преобразованными данными с помощью обыкновенного
- 127. Метод 4. Метод Хилдрета-Лу. Основан на тех же принципах, что и рассмотренный метод 3, но использует
- 129. Скачать презентацию

























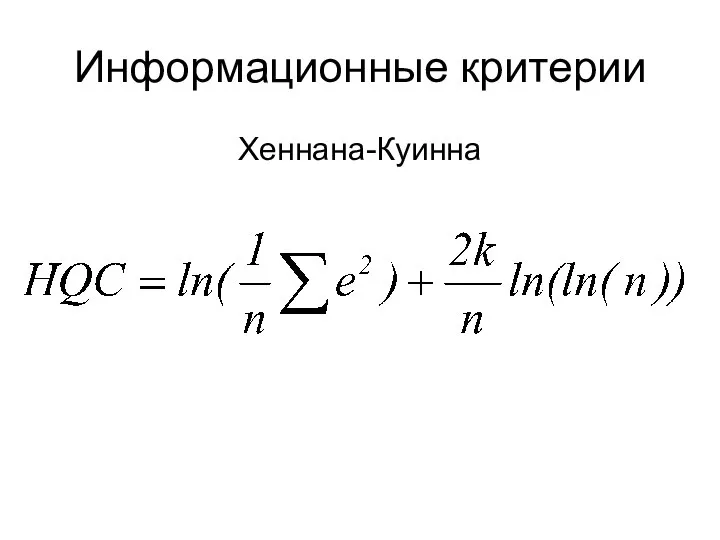





























































































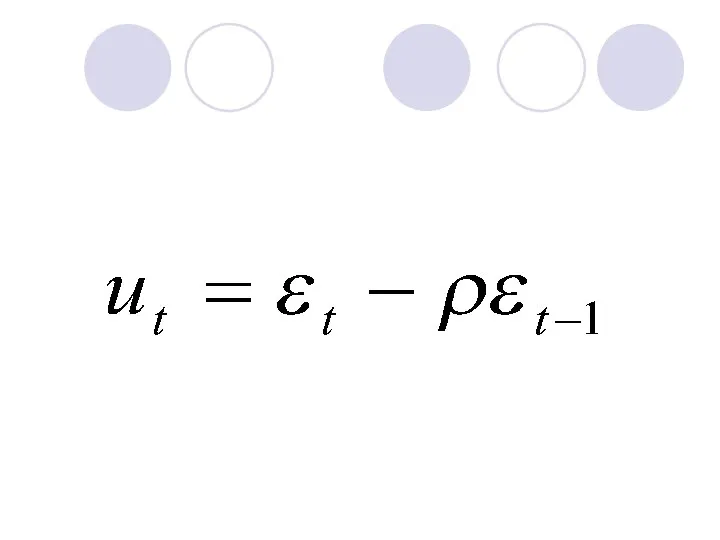






 Первый признак равенства треугольников
Первый признак равенства треугольников Евклид - древнегреческий математик
Евклид - древнегреческий математик  Winston p. 313
Winston p. 313 Интерактивные "Крестики-нолики". Задачи на готовых чертежах. Сумма углов треугольника
Интерактивные "Крестики-нолики". Задачи на готовых чертежах. Сумма углов треугольника Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Аттестационная работа. Элективный курс Теория чисел
Аттестационная работа. Элективный курс Теория чисел Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Математические игры по-олимпийски
Математические игры по-олимпийски Деление и умножение дробей
Деление и умножение дробей Устный счет. Линейная функция
Устный счет. Линейная функция Рациональные и иррациональные числа
Рациональные и иррациональные числа Ике турының параллельлек билгеләре
Ике турының параллельлек билгеләре Математика в музыке Автор: Филяровская Мария 4б класс
Математика в музыке Автор: Филяровская Мария 4б класс График функции
График функции Признаки параллельности прямых. Решение задач на готовых чертежах
Признаки параллельности прямых. Решение задач на готовых чертежах Задачи с практическим содержанием. Задания В1 ЕГЭ по математике
Задачи с практическим содержанием. Задания В1 ЕГЭ по математике Прямая в пространстве
Прямая в пространстве Статистические наблюдения
Статистические наблюдения Математика. 1 класс. Выдумки кляксы
Математика. 1 класс. Выдумки кляксы Мультиколлинеарность. Строгая и нестрогая мультиколлинеарность
Мультиколлинеарность. Строгая и нестрогая мультиколлинеарность Методика изучения двумерных геометрических фигур: виды углов; ломаная, многоугольники и их виды; прямоугольник, квадрат
Методика изучения двумерных геометрических фигур: виды углов; ломаная, многоугольники и их виды; прямоугольник, квадрат Презентация по математике "Путешествие в царство математики" - скачать
Презентация по математике "Путешествие в царство математики" - скачать  Площадь многоугольника. Свойства площадей
Площадь многоугольника. Свойства площадей Решение дифференциальных уравнений. (Лекция 6)
Решение дифференциальных уравнений. (Лекция 6) Решение задач с помощью линейных уравнений
Решение задач с помощью линейных уравнений Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Кубические и биквадратные уравнения
Кубические и биквадратные уравнения