Линейная алгебра. Матрицы

Матрицы

Матрицей размерности m x n называется прямоугольная таблица чисел, содержащая m

Матрица, все элементы которой равны нулю, называется нулевой и обозначается через

Единичная матрица Е – это диагональная матрица, в которой все

Пример

Пример

Пример

Вычислить 4А - 3B, если

Решение:

4А - 3B = 4А +

4. Умножение матриц

Опр. 17. Произведение матрицы А на матрицу В, определено

Найти произведение матриц АB и BA

Решение:
Произведение матриц АB существует, т.к. матрица

ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ

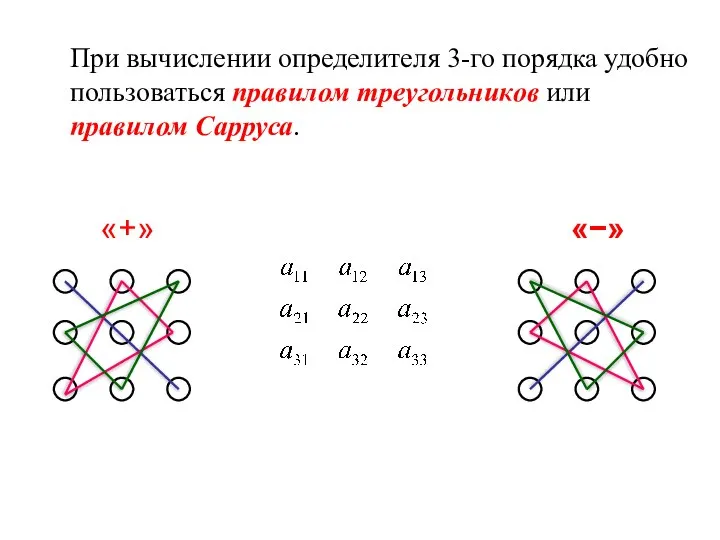
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников или правилом

Пример

Вычислить определители матриц:

Опр.2. Минором элемента aij матрицы  n-го  порядка A называется определитель матрицы

Пример. Найти миноры M11, M32, M43

Опр.4. Алгебраическим дополнением элемента аij  матрицы  n-го порядка А называется число,

Определитель n-го порядка матрицы Аn равен сумме произведений элементов любой строки

Пример

По 2-ой строке:

Пример

По 3-му столбцу:

Определитель n-го порядка треугольной матрицы равен произведению элементов главной диагонали.

Определитель n-го

Ранг матрицы

Элементарными преобразования матрицы называются :
Транспонирование (замена строк столбцами)
Перестановка строк и столбцов.
Умножение

Теорема о ранге матрицы

ОБРАТНАЯ МАТРИЦА

Опр. 1. Матрица А-1 называется обратной для квадратной матрицы А, если
АА-1

Всякая невырожденная матрица Аn имеет обратную матрицу А-1, причем
где Аij –

Пример

Найти матрицу, обратную к данной:

Решение:
Т.к. |А|=-2≠0, то матрица А – невырожденная

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Опр. Системой m линейных уравнений с n неизвестными (СЛУ) называется система

Опр. Матрица А составленная из коэффициентов СЛУ называется основной матрицей системы.

Опр. Матрицы X и B называются матрицы-столбцы неизвестных и свободных членов.

Матричная форма записи СЛУ:

Пример. Записать в матричной форме

Решение

Обозначим
Следовательно, имеем AX = B.

Рассмотрим частный случай неоднородной системы, когда m=n, т.е. систему вида

Определитель |А|

Пример. Решить систему

Решение.

т.е. исходная система трех неоднородных линейных уравнений с тремя неизвестными имеет

Следовательно, обратная матрица равна

Найдем теперь решение системы

Проверка

Правило Крамера

Согласно правилу Крамера, если |A| ≠ 0, то единственное решение

Найдем теперь решение системы по правилу Крамера

МЕТОД ГАУССА

Элементарными называются следующие преобразования системы:
Перестановка местами двух уравнений системы.
Умножение некоторого уравнения