Содержание
- 2. Числовые сравнения. Понятие сравнения Определение 1 Целые числа a и b называются сравнимыми по модулю m,
- 3. Теорема 1 Следующие утверждения равносильные: (1) (2) существует t ϵ Z ,что (3) a и b
- 4. Доказательство Докажем, что из (1) следует (2). По определению имеем: 2. Докажем, что из (2) следует
- 5. Определение 2 Числа a и b называются сравнимыми по модулю m, если они имеют одинаковые остатки
- 6. Основные свойства сравнений 1. (рефлексивность) для любого 2. (симметричность) Если ,то 3. (транзитивность) Если и ,
- 7. 4. Если , , то Доказательство Если ,то Следовательно, 5. Любое слагаемое сравнения можно переносить в
- 8. 6. Обе части сравнения можно умножать на одно и то же целое число, т.е.если ,то Доказательство
- 9. 8. Сравнения по одному и тому же модулю можно почленно перемножать Доказательство (свойство 6) Тогда по
- 10. 11. Обе части сравнения и модуль можно умножить на одно и то же натуральное число ,
- 11. 13. Обе части сравнения можно разделить на их общий множитель, если он взаимно прост с модулем
- 13. Скачать презентацию










 Задания по математике. (Вариант 7)
Задания по математике. (Вариант 7) Презентация по математике Признаки параллельных прямых
Презентация по математике Признаки параллельных прямых  Умножение натуральных чисел
Умножение натуральных чисел Путешествие в страну знаний
Путешествие в страну знаний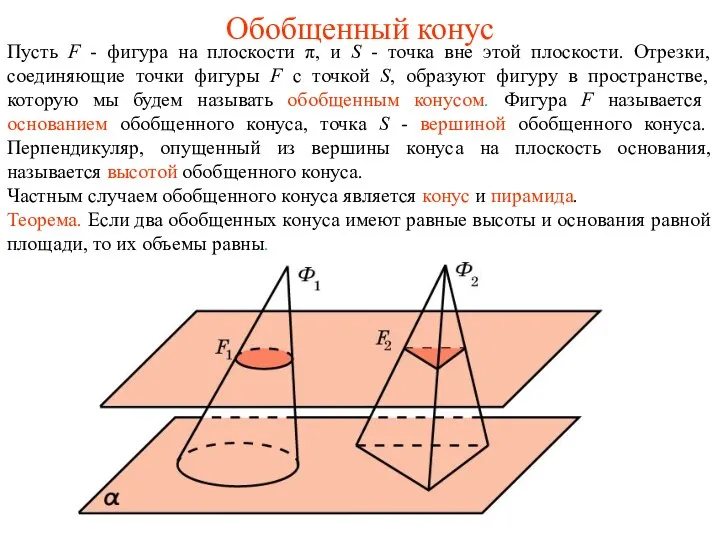 Объем пирамиды
Объем пирамиды Непериодические бесконечные десятичные дроби. Часть 2
Непериодические бесконечные десятичные дроби. Часть 2 Определение числовой функции и способы её задания
Определение числовой функции и способы её задания Презентация на тему Пропорциональные величины
Презентация на тему Пропорциональные величины  Статистические оценки
Статистические оценки Старинный способ решения задач на смеси и сплавы
Старинный способ решения задач на смеси и сплавы Построение перпендикулярных прямых
Построение перпендикулярных прямых Смотр подготовила и провела учитель математики высшей категории МОУ- Ивановской СОШ Баганского района НСО Иваненко ОВ 2007/2008 уч
Смотр подготовила и провела учитель математики высшей категории МОУ- Ивановской СОШ Баганского района НСО Иваненко ОВ 2007/2008 уч Какую прямую называют координатной?
Какую прямую называют координатной? Треугольники. Решение задач
Треугольники. Решение задач Овоид
Овоид Математическое обеспечение финансовых решений
Математическое обеспечение финансовых решений Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Симметрия в природе
Симметрия в природе Логическое следование
Логическое следование Производная функции
Производная функции Увеличение числа на несколько единиц. Примеры
Увеличение числа на несколько единиц. Примеры Преобразование графиков функции
Преобразование графиков функции Параллельные прямые. Их признаки и свойства
Параллельные прямые. Их признаки и свойства Чтение графика функции
Чтение графика функции Метрология. Введение. Структура дисциплины
Метрология. Введение. Структура дисциплины Сумма углов треугольника
Сумма углов треугольника Предварительный эксперимент и методы его анализа
Предварительный эксперимент и методы его анализа Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом.
Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом.