Статистические оценки параметров распределения случайных величин по выборкам. Вариационные ряды и их графики
Содержание
- 2. Вариационные ряды и их графики дают наглядное представление о варьировании признаков, но они недостаточны для полного
- 3. К числу важнейших показателей, используемых в статистическом анализе, относят: 1) средние величины; 2) показатели разнообразия и
- 4. В зависимости от того, как распределены первичные данные – в равно- или в неравноинтервальный вариационный ряд
- 5. Средние величины. В отличие от индивидуальных числовых характеристик средние величины обладают большей устойчивостью, способностью характеризовать целую
- 6. Показатели средних величин обладают следующими свойствами: являются обобщенными статистическими параметрами, они позволяют получать срединное значение варьирующего
- 7. средние величины могут характеризовать только однородную совокупность вариант; одни средние применяются только в симметричных рядах (арифметическая,
- 8. Структурные средние и способы их вычисления. Структурные величины представляют собой конкретные варианты имеющейся совокупности, которые занимают
- 9. При нормальном распределении величины моды (Mo), медианы (Ме) и средней арифметической ( ) равны . Чем
- 10. В качестве примера рассмотрим распределение, представленное в таблице 4.1. Таблица 4.1.
- 11. В этом распределении наиболее многочисленным является пятый класс (180-199 с частотой 250. Это модальный класс. Формула
- 27. Скачать презентацию
























 Логарифмы на ЕГЭ
Логарифмы на ЕГЭ Площадь фигуры. Измерение и единицы площади
Площадь фигуры. Измерение и единицы площади Сложение и вычитание десятичных дробей. Урок с использованием интерактивной доски
Сложение и вычитание десятичных дробей. Урок с использованием интерактивной доски Весёлая математика
Весёлая математика Аттестационная работа. Решение текстовых задач» Элективный курс по математике для 9 класса
Аттестационная работа. Решение текстовых задач» Элективный курс по математике для 9 класса Второй признак равенства треугольников
Второй признак равенства треугольников Великий древнегреческий математик Пифагор
Великий древнегреческий математик Пифагор Сумма углов треугольника
Сумма углов треугольника Таблица сложения в пределах 20
Таблица сложения в пределах 20 Проверка умножения
Проверка умножения Стандартный вид числа
Стандартный вид числа Умножение десятичных дробей. Деление десятичных дробей на натуральное число. 5 класс
Умножение десятичных дробей. Деление десятичных дробей на натуральное число. 5 класс Дискриминантный анализ Фишера с kernel trick
Дискриминантный анализ Фишера с kernel trick Правильные многоугольники
Правильные многоугольники Признаки подобия треугольников. Решение задач
Признаки подобия треугольников. Решение задач Параллельность прямой и плоскости
Параллельность прямой и плоскости Величины, длина
Величины, длина Путешествия на тропинках математики
Путешествия на тропинках математики Презентация на тему Подобные треугольники
Презентация на тему Подобные треугольники  Аттестационная работа. Методическая разработка исследовательской работы «Длина окружности и площадь круга». (6 класс)
Аттестационная работа. Методическая разработка исследовательской работы «Длина окружности и площадь круга». (6 класс) Проверка гипотез. Выборки. (Часть 2)
Проверка гипотез. Выборки. (Часть 2) Перетворення та переміщення подібності. (9 клас)
Перетворення та переміщення подібності. (9 клас)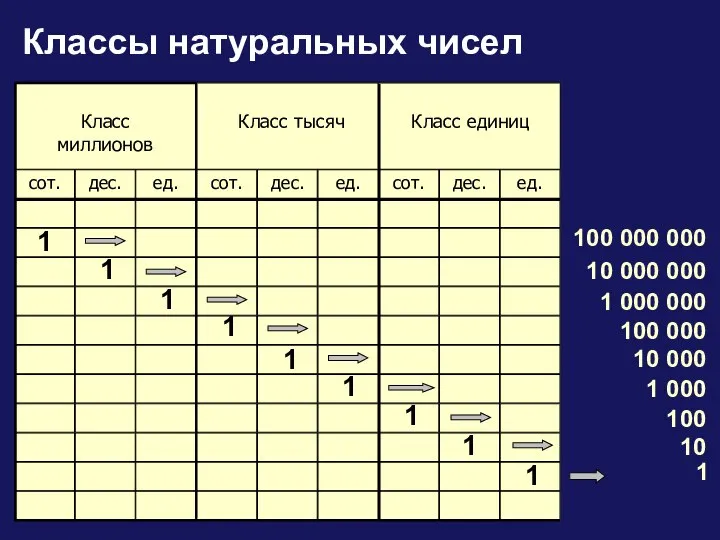 Классы натуральных чисел
Классы натуральных чисел Метрология. Объекты метрологии
Метрология. Объекты метрологии Презентация по математике "Распределительный закон умножения относительно сложения" - скачать бесплатно
Презентация по математике "Распределительный закон умножения относительно сложения" - скачать бесплатно Корреляционный анализ
Корреляционный анализ Презентация по математике "ВЕСЕЛАЯ МАТЕМАТИКА" - скачать
Презентация по математике "ВЕСЕЛАЯ МАТЕМАТИКА" - скачать  Презентация по математике "Математическое образование в петровскую эпоху" - скачать
Презентация по математике "Математическое образование в петровскую эпоху" - скачать