Кристаллография. Точечные группы симметрии, принцип их вывода с помощью понятия о группах. Формы кристаллов низшей категории

Полная совокупность элементов симметрии кристаллического
многогранника называется видом симметрий, или точечной группой
симметрии.

Вектора после равенства являются компонентами вектора d
а данное выражение его

Преобразование базиса -
преобразование системы координат с сохранением начала координат

Пусть исходный

Если фигура составлена из равных частей, равно расположенных друг
относительно друга,

Центр инверсии

Центр инверсии

Плоскость симметрии

Плоскость симметрии

Плоскость симметрии

Поворотные оси симметрии

1

-1

2

-2

3

-3

4

-4

6

-6

Поворотные оси симметрии

L1

Поворотные оси симметрии

L2

Поворотные оси симметрии

L4

Поворотные оси симметрии

L2

инверсионные оси симметрии

-2

-4

Неортогональные системы координат

a=b≠c, α=β=900, γ=1200

L33L23M
тригональная
голоэдрия

L66L27mc
гексагональная
голоэдрия

Гексагональная сингония

6/mmm

Гексагональная сингония

Гексагональная сингония

Гексагональная сингония

Гексагональная сингония

Тригональная сингония

Тригональная сингония

Свойства матриц

Перемножение матриц

Произведением двух матриц А = αik строения m×n и

Свойства матриц

Перемножение матриц

Свойства матриц

Перемножение матриц

Умножение матриц

Теорема Эйлера и следствия

Поворот вокруг двух пересекающихся осей эквивалентен
повороту вокруг

Теорема Эйлера и следствия

Если поворотную ось симметрии n порядка пересекает перпендикулярная

Теорема Эйлера и следствия

4 оси 2 порядка
под углом
360/8 = 45

Теорема Эйлера и следствия

Если через поворотную ось симметрии порядка n проходит

Теорема Эйлера и следствия

4 плоскости m проходящие под 45 градусов
относительно

Группа

Множество G отличных друг от друга элементов называется
группой, если выполнены

Группа

Например:

Существует алгебраическое действие, которое каждой упорядоченной паре элементов
g1 и g2 из

Группа

В кристаллографии группой является совокупность элементов
преобразования симметрии, совмещающая фигуру саму

Группа

Покажем, для группы 222 выполняются все 4 аксиомы

Такая запись получила
название квадрат Кейли

Существует алгебраическое действие, которое каждой упорядоченной

Умножение матриц, элементами которых являются числа ассоциативно по определению

Умножение ассоциативно, т.е.

Тригональная сингония

Планальный вид симметрии

Эта группа может быть получена при помощи
2-х элементов

Доказать все аксиомы без квадрата Кейли

Покажем, что

Покажем, что

Группы низшей категории

Триклинная
сингония

1

-1

моноклинная
сингония

2

m

2/m

222

mm2

mmm

ромбическая
сингония

Группы низшей категории

mm2

1 =

Группы низшей категории

mm2

Группы низшей категории

mm2

Группы низшей категории

mmm

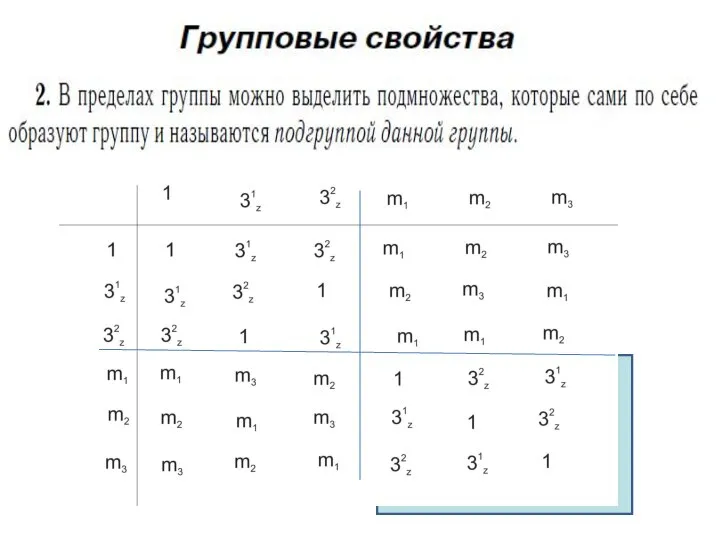
1
31z
32z
m1
m2
m3

порядок равен
6

Порядок точечной группы равен количеству граней, которые
порождаются из

Теорема Лагранжа

Если G – группа конечного порядка и H

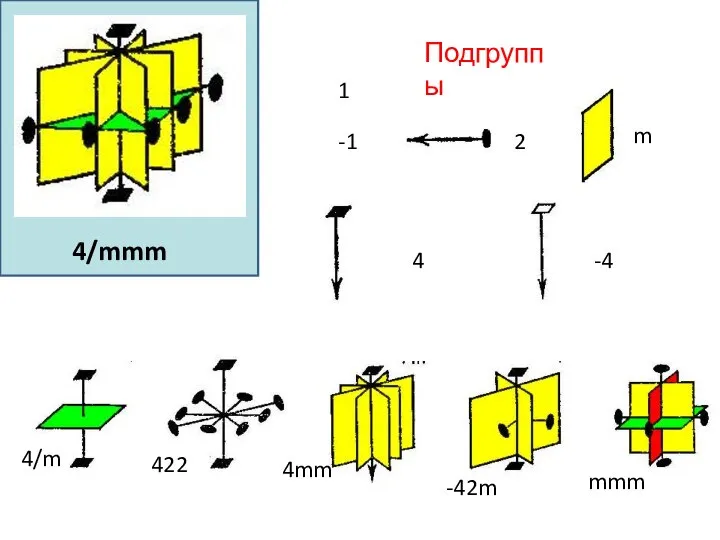
4/mmm

Подгруппы

4

-4

4/m

422

4mm

-42m

mmm

1

2

m

-1

Группа является коммутативной или абелевой, если групповое
действие коммутативно для всех

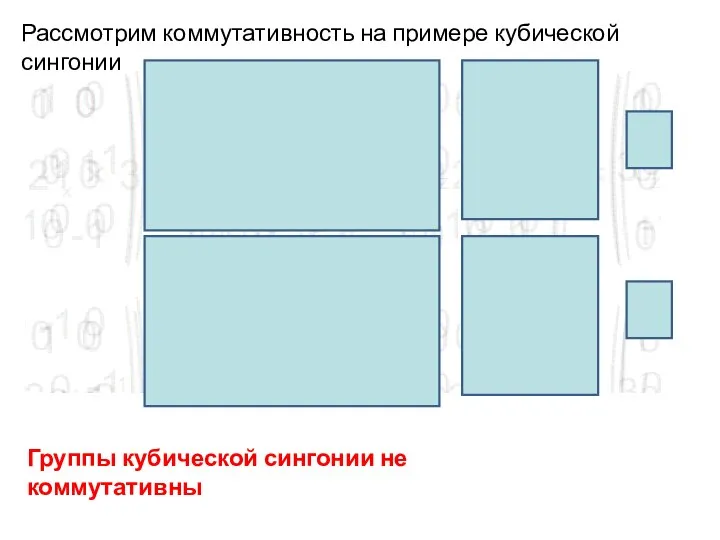
Рассмотрим коммутативность на примере кубической сингонии

Группы кубической сингонии не коммутативны

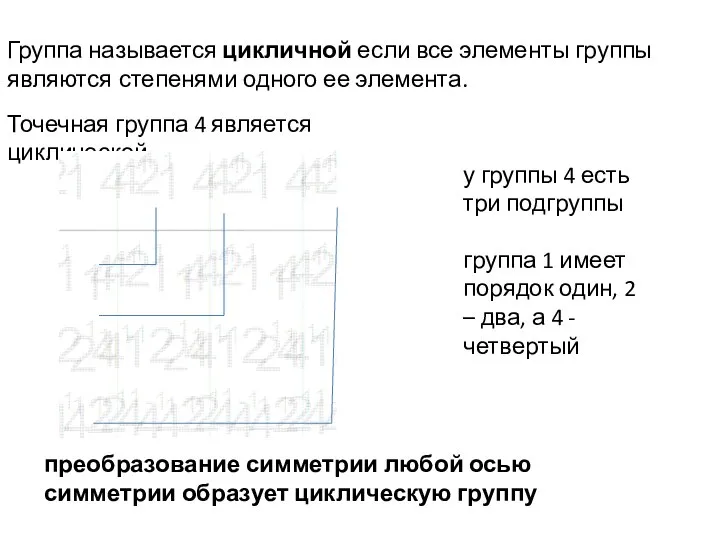
Группа называется цикличной если все элементы группы
являются степенями одного ее

Найдем квадрат Кейли для осей 6 и -6.

6

-6

61

62

63

64

65

1

-61

-62

-63

-64

-65

1

Найдем квадрат Кейли для осей 6 и -6.

Найдем квадрат Кейли для осей 6 и -6.

Вывод точечных групп симметрии

выведем группы моноклинной и ромбической сингонии

в моноклинной

Появился новый элемент симметрии mz

Значит множество не замкнуто относительно умножения

Добавляем mz

Добавляем к группе 2 (2, 2z) преобразование 2x и получаем новое