Содержание
- 2. Содержание Алгоритм Лианга—Барского
- 3. Алгоритм Лианга—Барского Лианг и Барский предложили алгоритмы отсечения прямоугольным окном с использованием параметрического представления для двух-,
- 5. Параметрическое представление Отсекаемый отрезок прямой может быть преобразован в параметрическое представление следующим образом. Пусть конечные точки
- 6. Параметрическое представление Подставляя параметрическое представление, заданное уравнениями (3.2) и (3.3), в неравенства (3.1), получим следующие соотношения
- 7. Анализ неравенств По определению внутренней и внешней стороны линии границы заметим, что каждое из неравенств (3.5)
- 8. Анализ неравенств Рассмотрим Pi в соотношениях (3.6). Возможны три случая: • Pi t ⩾Qi/Pi. (3.7) Очевидно,
- 9. Условия видимости Геометрически, если Pi = 0, то нет точек пересечения удлиненной линии, определяемой точками V0V1,
- 11. Скачать презентацию
Слайд 2
Содержание
Алгоритм Лианга—Барского
Содержание
Алгоритм Лианга—Барского
Слайд 3
Алгоритм Лианга—Барского
Лианг и Барский предложили алгоритмы отсечения прямоугольным окном с использованием
Алгоритм Лианга—Барского
Лианг и Барский предложили алгоритмы отсечения прямоугольным окном с использованием
параметрического представления для двух-, трех-и четырехмерного отсечения.
В частности, внутренняя часть окна отсечения может быть выражена
с помощью следующих неравенств:
xлeв ⩽ x ⩽ xпpaв;
yвepx ⩽ y ⩽ yниз. (3.1)
Продолжим каждую из четырех границ окна до бесконечных прямых.
Каждая из таких прямых делит плоскость на две области. Назовем «видимой частью» ту, в которой находится окно отсечения.
Видимой части соответствует внутренняя сторона линии границы.
Невидимой части плоскости соответствует внешняя сторона линии границы.
Таким образом, окно отсечения может быть определено как
область, которая находится на внутренней стороне всех линий границ.
В частности, внутренняя часть окна отсечения может быть выражена
с помощью следующих неравенств:
xлeв ⩽ x ⩽ xпpaв;
yвepx ⩽ y ⩽ yниз. (3.1)
Продолжим каждую из четырех границ окна до бесконечных прямых.
Каждая из таких прямых делит плоскость на две области. Назовем «видимой частью» ту, в которой находится окно отсечения.
Видимой части соответствует внутренняя сторона линии границы.
Невидимой части плоскости соответствует внешняя сторона линии границы.
Таким образом, окно отсечения может быть определено как
область, которая находится на внутренней стороне всех линий границ.
Слайд 4
Слайд 5
Параметрическое представление
Отсекаемый отрезок прямой может быть преобразован в параметрическое представление следующим
Параметрическое представление
Отсекаемый отрезок прямой может быть преобразован в параметрическое представление следующим
образом.
Пусть конечные точки отрезка есть V0 и V1 с координатами (x0, y0) и (x1, y1) соответственно
Тогда параметрическое представление линии может быть задано следующим
образом:
x = x0 + dx ⋅ t; y = y0 + dy ⋅ t. (3.2)
dx = x1 − x0; dy = y1 − y0.
Или в общем виде для отрезка, заданного точками V0 и V1:
V(t) = V0 + (V1 − V0) ⋅ t. (3.3)
Для точек V0 и V1 параметр t равен 0 и 1 соответственно.
Меняя t от 0 до 1, перемещаемся по отрезку V0V1 от точки V0 к точке V1.
Изменяя t в интервале [−1, 1], получаем бесконечную прямую, ориентация которой — от точки V0 к точке V1.
Пусть конечные точки отрезка есть V0 и V1 с координатами (x0, y0) и (x1, y1) соответственно
Тогда параметрическое представление линии может быть задано следующим
образом:
x = x0 + dx ⋅ t; y = y0 + dy ⋅ t. (3.2)
dx = x1 − x0; dy = y1 − y0.
Или в общем виде для отрезка, заданного точками V0 и V1:
V(t) = V0 + (V1 − V0) ⋅ t. (3.3)
Для точек V0 и V1 параметр t равен 0 и 1 соответственно.
Меняя t от 0 до 1, перемещаемся по отрезку V0V1 от точки V0 к точке V1.
Изменяя t в интервале [−1, 1], получаем бесконечную прямую, ориентация которой — от точки V0 к точке V1.
Слайд 6
Параметрическое представление
Подставляя параметрическое представление, заданное уравнениями (3.2) и (3.3),
в неравенства (3.1),
Параметрическое представление
Подставляя параметрическое представление, заданное уравнениями (3.2) и (3.3),
в неравенства (3.1),
получим следующие соотношения для частей удлиненной ли-
нии, которая находится в окне отсечения:
−dx ⋅ t ⩽ x0 − xлeв; dx ⋅ t ⩽ xпpaв − x0;
−dy ⋅ t ⩽ y0 − yниз; dy ⋅ t ⩽ yвepx − y0. (3.4)
Заметим, что соотношения (3.4) — неравенства, описывающие внутреннюю часть
окна отсечения, в то время как равенства определяют его границы.
Рассматривая неравенства (3.4), видим, что они имеют одинаковую форму вида:
Pi ⋅ t ⩽ Qi, (3.5)
где i = 1, 2, 3, 4.
Здесь использованы следующие обозначения:
P1 = −dx; Q1 = x0 − xлeв; P3 = −dy; Q3 = y0 − yниз;
P2 = dx; Q2 = xпpaв − x0; P4 = dy; Q4 = yвepx − y0. (3.6)
нии, которая находится в окне отсечения:
−dx ⋅ t ⩽ x0 − xлeв; dx ⋅ t ⩽ xпpaв − x0;
−dy ⋅ t ⩽ y0 − yниз; dy ⋅ t ⩽ yвepx − y0. (3.4)
Заметим, что соотношения (3.4) — неравенства, описывающие внутреннюю часть
окна отсечения, в то время как равенства определяют его границы.
Рассматривая неравенства (3.4), видим, что они имеют одинаковую форму вида:
Pi ⋅ t ⩽ Qi, (3.5)
где i = 1, 2, 3, 4.
Здесь использованы следующие обозначения:
P1 = −dx; Q1 = x0 − xлeв; P3 = −dy; Q3 = y0 − yниз;
P2 = dx; Q2 = xпpaв − x0; P4 = dy; Q4 = yвepx − y0. (3.6)
Слайд 7
Анализ неравенств
По определению внутренней и внешней стороны линии границы заметим, что
каждое
Анализ неравенств
По определению внутренней и внешней стороны линии границы заметим, что
каждое
из неравенств (3.5) соответствует одной из граничных линий (левой, правой, нижней и верхней соответственно) и описывает ее видимую сторону. Удлиним V0V1 в бесконечную прямую.
Тогда каждое неравенство задает диапазон значений параметра t, для которых эта удлиненная линия находится на видимой стороне соответствующей линии границы.
Более того, конкретное значение параметра t для точки пересечения есть t = Qi/Pi.
Причем знак Qi показывает, на какой стороне соответствующей линии границы находится точка V0. А именно, если Qi > 0, тогда
V0 находится на видимой стороне линии границы, включая и ее. Если же Qi < 0, тогда V0 находится на невидимой стороне.
Тогда каждое неравенство задает диапазон значений параметра t, для которых эта удлиненная линия находится на видимой стороне соответствующей линии границы.
Более того, конкретное значение параметра t для точки пересечения есть t = Qi/Pi.
Причем знак Qi показывает, на какой стороне соответствующей линии границы находится точка V0. А именно, если Qi > 0, тогда
V0 находится на видимой стороне линии границы, включая и ее. Если же Qi < 0, тогда V0 находится на невидимой стороне.
Слайд 8
Анализ неравенств
Рассмотрим Pi в соотношениях (3.6). Возможны три случая:
• Pi <
Анализ неравенств
Рассмотрим Pi в соотношениях (3.6). Возможны три случая:
• Pi <
0, тогда соответствующее неравенство становится:
t ⩾Qi/Pi. (3.7)
Очевидно, что диапазон значений параметра t, для которых удлиненная
линия находится на видимой стороне соответствующей граничной линии,
имеет минимум в точке пересечения направленной удлиненной линии, заданной вектором V0V1, и идущей с невидимой на видимую сторону граничной линии.
Pi > 0, тогда соответствующее неравенство становится:
t ⩽ Qi/Pi. (3.8)
Так как значения параметра t только на границе равны Qi/Pi, а в остальной видимой части меньше Qi/Pi, то значение параметра t имеет максимум на границе.
• Pi = 0, тогда соответствующее неравенство превращается в
0 ⩽ Qi.
t ⩾Qi/Pi. (3.7)
Очевидно, что диапазон значений параметра t, для которых удлиненная
линия находится на видимой стороне соответствующей граничной линии,
имеет минимум в точке пересечения направленной удлиненной линии, заданной вектором V0V1, и идущей с невидимой на видимую сторону граничной линии.
Pi > 0, тогда соответствующее неравенство становится:
t ⩽ Qi/Pi. (3.8)
Так как значения параметра t только на границе равны Qi/Pi, а в остальной видимой части меньше Qi/Pi, то значение параметра t имеет максимум на границе.
• Pi = 0, тогда соответствующее неравенство превращается в
0 ⩽ Qi.
Слайд 9
Условия видимости
Геометрически, если Pi = 0, то нет точек пересечения удлиненной
Условия видимости
Геометрически, если Pi = 0, то нет точек пересечения удлиненной
линии, определяемой точками V0V1, с линиями границы.
Более того, если Qi < 0, то удлиненная линия находится на внешней стороне линии границы, а при Qi ⩾ 0 находится на внутренней стороне (включая ее).
В последнем случае отрезок V0V1 может быть видим или нет, в зависимости от того, где находятся точки V0V1 на удлиненной линии.
В предыдущем же случае нет видимого сегмента, так как удлиненная линия вне окна, т. е. это случай тривиального отбрасывания.
Итак, рассмотрение неравенств дает диапазон значений параметра t, для которого удлиненная линия находится внутри окна отсечения.
Более того, если Qi < 0, то удлиненная линия находится на внешней стороне линии границы, а при Qi ⩾ 0 находится на внутренней стороне (включая ее).
В последнем случае отрезок V0V1 может быть видим или нет, в зависимости от того, где находятся точки V0V1 на удлиненной линии.
В предыдущем же случае нет видимого сегмента, так как удлиненная линия вне окна, т. е. это случай тривиального отбрасывания.
Итак, рассмотрение неравенств дает диапазон значений параметра t, для которого удлиненная линия находится внутри окна отсечения.
- Предыдущая
Пример расчёта сейсмики резервуараСледующая -
Темы проектов по разным предметам







 Черчение. Оформление чертежа
Черчение. Оформление чертежа Соединение вида и разреза
Соединение вида и разреза Технический рисунок. Основы дисциплины, цели, средства и материалы. Основы архитектурного черчения. Масштабы, линии чертежа
Технический рисунок. Основы дисциплины, цели, средства и материалы. Основы архитектурного черчения. Масштабы, линии чертежа Резьбы. Стандартные крепёжные детали
Резьбы. Стандартные крепёжные детали Базовые ГОСТы. ГОСТ 2.301-68. Форматы
Базовые ГОСТы. ГОСТ 2.301-68. Форматы Балки составного сечения: конструкция и расчёт
Балки составного сечения: конструкция и расчёт Історія розвитку графіки. Креслярські інструменти та приладдя
Історія розвитку графіки. Креслярські інструменти та приладдя Нанесение размеров
Нанесение размеров Чертежный шрифт
Чертежный шрифт Архитектурно-строительное черчение
Архитектурно-строительное черчение Развертки поверхностей
Развертки поверхностей Нанесение размеров с учетом формы предмета
Нанесение размеров с учетом формы предмета Черчение. Оформление чертежа
Черчение. Оформление чертежа Створення креслень в КОМПАС-3D V14/16
Створення креслень в КОМПАС-3D V14/16 Правила нанесения размеров на чертежах. Масштаб. Урок 5
Правила нанесения размеров на чертежах. Масштаб. Урок 5 Эскизирование детали Крышка
Эскизирование детали Крышка Графическая, конструкторская и технологическая документация проекта
Графическая, конструкторская и технологическая документация проекта Трубы из ПНД для дренажа
Трубы из ПНД для дренажа Расположение видов на чертеже
Расположение видов на чертеже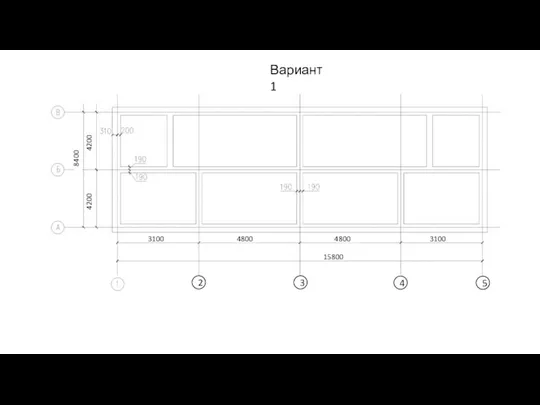 Варианты для чертежей
Варианты для чертежей Совершенствование технологии и организации окраски сельскохозяйственных машин в ЗАО Любань
Совершенствование технологии и организации окраски сельскохозяйственных машин в ЗАО Любань Общие требования и правила оформления текстовой, графической и конструкторской документации
Общие требования и правила оформления текстовой, графической и конструкторской документации Задание точки, прямой, плоскости и многогранников на комплексном чертеже
Задание точки, прямой, плоскости и многогранников на комплексном чертеже Графические элементы в пространстве
Графические элементы в пространстве Линии чертежа
Линии чертежа Выразительные средства графики
Выразительные средства графики Сечения. Вынесенные сечения
Сечения. Вынесенные сечения Модель поверхности
Модель поверхности